Conditions aux limites absorbantes pour les objets allongés

Hélène Barucq, M'Barek Fares, Anne-Gaëlle Dupouy Saint-Guirons et Sébastien Tordeux

Lorsque l’on cherche à calculer le champ diffracté par un objet rigide, il est classique de restreindre le domaine de calcul à une boule de rayon R et de poser des conditions absorbantes sur sa frontière. Ce choix de frontière fictive n’est pas du tout optimal lorsque l’objet diffractant est allongé dans une direction. Nous avons montré qu’il est possible de construire des conditions aux limites absorbantes d’ordre arbitraire sur une frontière sphéroïdale en dimension 3.



Les publications :



Exposé :

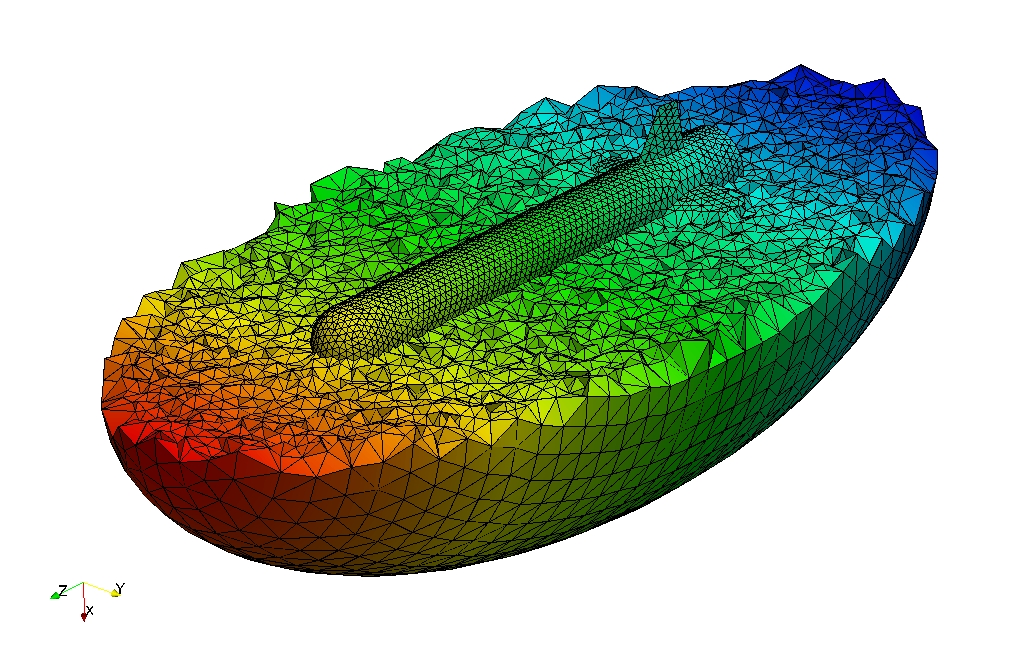
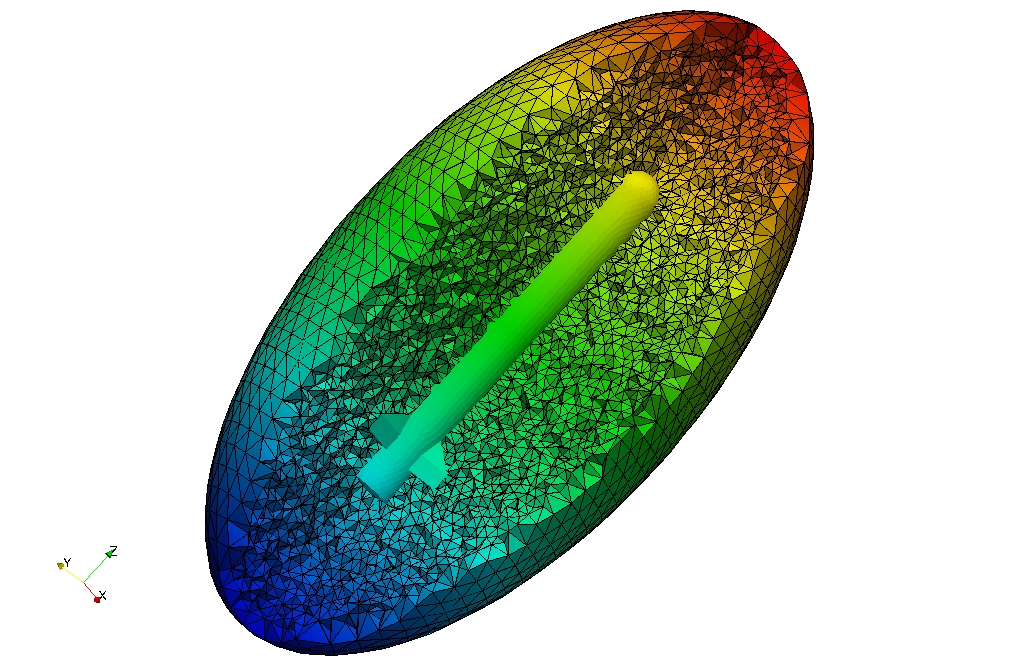
Un exemple : Calcul du diagramme de rayonnement d'une fusée





Nous comparons ici les résultats de notre méthode numérique à une solution de référence obtenue par le code CESC du Cerfacs. Nous représentons sur la sphère unité les approximations numériques obtenues par notre méthode de la SER de la fusée, en fonction du nombre de modes



SER de référence




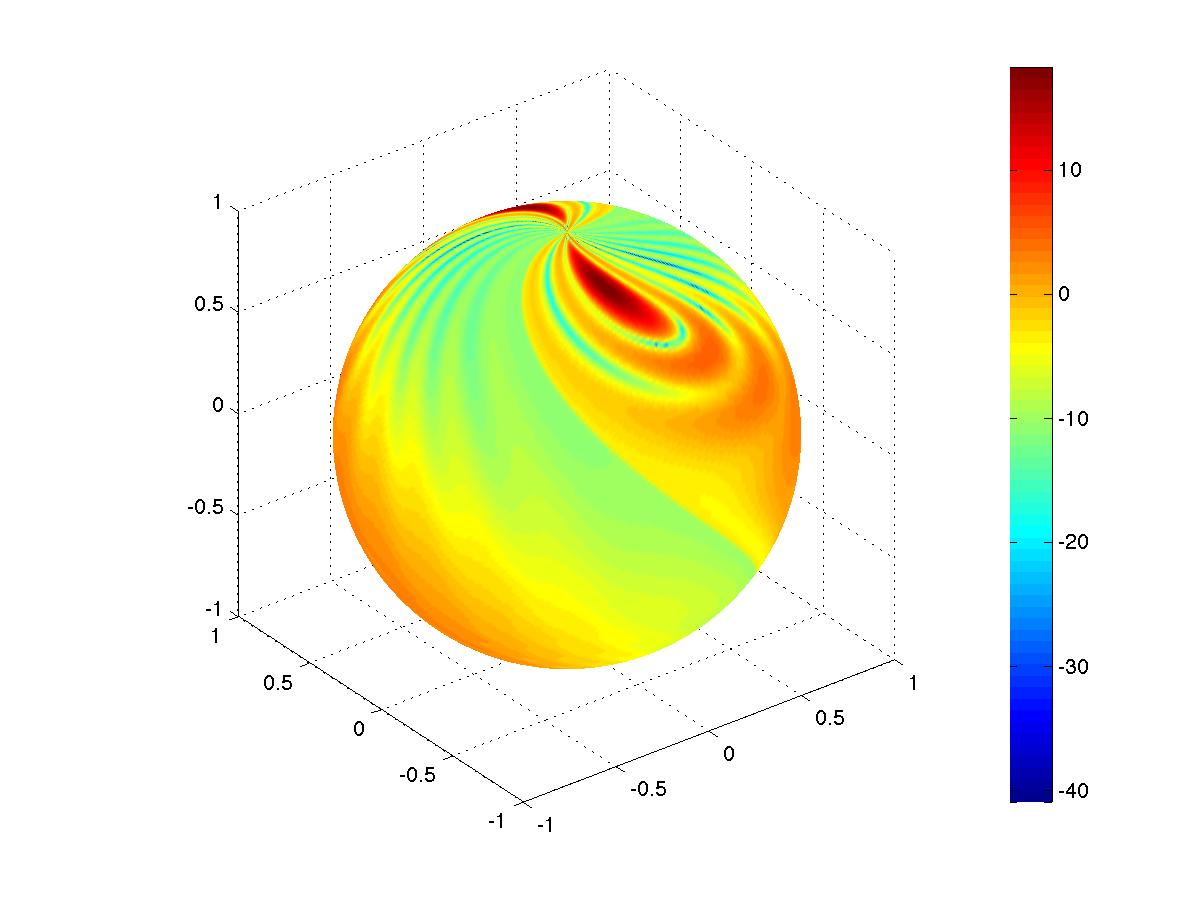
SER en dB pour la CLA d'ordre 1 (à gauche) et l'erreur face à la solution de référence (à droite)



SER en dB pour la CLA d'ordre 5 (à gauche) et l'erreur face à la solution de référence (à droite)



SER en dB pour la CLA d'ordre 20 (à gauche) et l'erreur face à la solution de référence (à droite)





Coupe de la SER en db en theta = 60 degré

Nous comparons ici une coupe de l'approximation de la SER à la SER de référence calculée par CESC






Les fonctions sphéroïdales angulaires

Lors de ce projet, il a été nécessaire de calculer les foncions sphéroïdales angulaire de première espèce. Nous représentons la partie réelle des premières sphéroïdales Ymn:

m=0 et n=0

m=0 et n=1

m=0 et n=2

m=0 et n=3

m=1 et n=0

m=1 et n=1

m=1 et n=2

m=1 et n=3

m=2 et n=0

m=2 et n=1

m=2 et n=2

m=2 et n=3

m=3 et n=0

m=3 et n=1

m=3 et n=2

m=3 et n=3

m=4 et n=0

m=4 et n=1

m=4 et n=2

m=4 et n=3

m=5 et n=0

m=5 et n=1

m=5 et n=2

m=5 et n=3